What is the Black Box Problem Actually?
Discussing why we can't understand how AI makes its decisions
In the past few years, we have witnessed a remarkable evolution in the capabilities of artificial intelligence (AI), particularly in the realm of multi-layer perceptrons (MLPs). These intricate models have demonstrated an impressive ability to perform a wide array of complex, narrow tasks with a level of proficiency that often rivals or even surpasses that of their human counterparts. Consequently, MLPs have emerged as a valuable tool for executing micro tasks and enhancing overall efficiency across an extensive range of industries and services.
However, as with any powerful technology, the increased capabilities of MLPs have also brought about a set of unique challenges and risks. One such concern is the potential for inaccurate or misleading outputs, which can arise from the "black box" nature of these models. The complexity of MLPs can make it difficult to understand the precise mechanisms and calculations that lead to a particular decision or prediction, thus complicating efforts to identify and correct errors.
Moreover, there is the risk of systemic harm, which can occur when the patterns and biases present in the training data are inadvertently perpetuated or amplified by the AI model. This can result in outputs that are not only incorrect but also unfair or discriminatory, with potentially serious consequences for the individuals or groups affected.
Why Does this Emerge?
The "black box" problem in neural networks (NNs) is a complex issue that arises from the mathematical emergence and uncertainty inherent in their operation. NNs are composed of interconnected nodes, or "neurons," that work together to produce an output when given a certain input. However, the way in which these neurons arrive at a particular output is not well understood, and is often referred to as a "black box."
The crux of the problem is that while we know that a set of neurons is being activated, we do not know the exact composition of this set. Furthermore, we have a limited understanding of how these neurons represent concepts or sub-concepts, or how they arrive at these representative states. The decisions made by the neurons, and the way they are understood and interpreted within the network, are shrouded in mystery. This lack of transparency and interpretability is a major obstacle to the widespread adoption and deployment of NNs in many domains.
One of the key challenges in addressing the "black box" problem is understanding the nature of the internal states and representations within NNs. It is unclear how these representations are formed, how they are related to the input and output of the network, and how they can be interpreted and understood by humans. Additionally, the highly distributed and non-linear nature of NNs makes it difficult to trace the flow of information and the transformation of representations as they propagate through the network. These challenges highlight the need for continued research and innovation in the field of NNs, in order to shed light on their inner workings and to develop more transparent and interpretable systems.
Explosion of Linear Surfaces
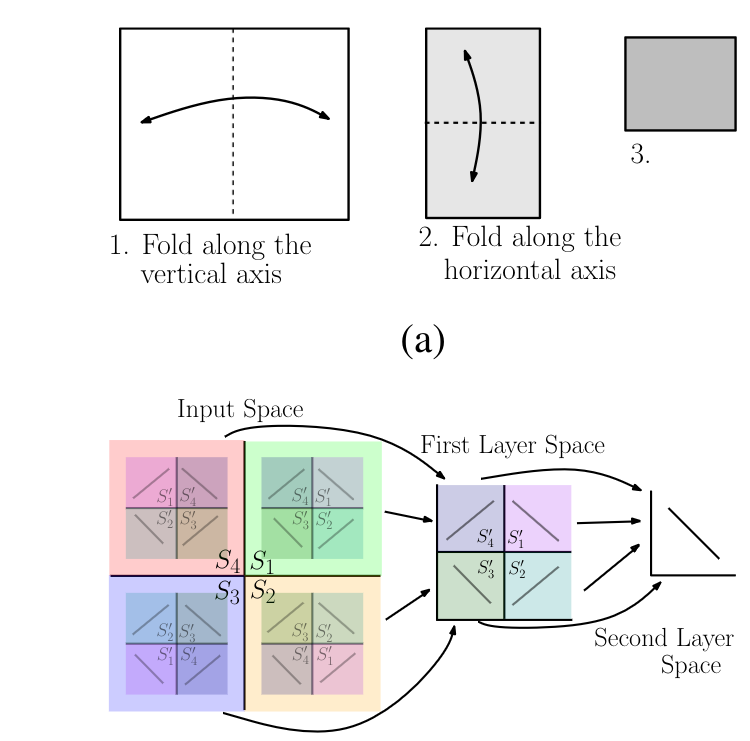
The fundamental concept behind the complexity of Deep Neural Networks (DNNs) lies in the exponential number of linear regions that need to be mapped onto the object feature space, which is significantly larger than the original expected feature space map. This is due to the permutability of the folding orders of the input space.
Each layer in a DNN applies a linear transformation to its input and passes it through a non-linear activation function. This process can be viewed as a folding operation, where each hidden layer folds the space of activations of the previous layer. Therefore, a DNN recursively folds its input space, starting from the first layer. The result of this recursive folding is that any function computed on the final folded space applies to all the collapsed subsets identified by the map corresponding to the succession of foldings. In simpler terms, any partitioning of the last layer's image-space is replicated in all input-space regions identified by the succession of foldings.
The space foldings in DNNs are not limited to foldings along coordinate axes and do not necessarily preserve lengths. Instead, the space is folded based on the orientations and shifts encoded in the input weights (W) and biases (b), and the non-linear activation function used at each hidden layer. This implies that the sizes and orientations of identified input-space regions may vary from each other, adding to the complexity and the "black box" nature of DNNs.
Non-Convex Optimization and Complexity
Non-convex optimization, which aims to achieve a global loss minimum in machine learning problems, enhances models' ability to capture intricate patterns within the input feature space. This complexity is attributed to the token landscape, which serves as a sophisticated mathematical representation of the input features, enabling models to significantly boost their expressive power and generalizability, even within high-dimensional spaces. The token landscape in non-convex optimization reflects multi-dimensional, non-linear relationships present in the data. Each token or feature represents a dimension in this high-dimensional space, and the interactions between these dimensions form a complex surface with numerous peaks and valleys. This intricate landscape allows models to learn highly detailed and nuanced representations of the data, capturing subtle patterns that simpler, convex models might miss. Non-convex models are particularly adept at handling high-dimensional input spaces, where each dimension can represent a unique feature or attribute of the data. The ability to navigate and optimize within these high-dimensional spaces enables the models to generalize well, capturing essential data structures and relationships that contribute to robust performance across diverse tasks.
However, the same complexity that augments the expressive power and generalizability of these models introduces significant challenges. Most algorithms employed in non-convex optimization rely heavily on heuristics, which are rule-based strategies or approximations designed to solve complex problems more efficiently. These heuristics are necessary because exact optimization in non-convex landscapes is computationally infeasible. Techniques such as stochastic gradient descent (SGD), simulated annealing, and genetic algorithms exemplify this heuristic reliance. While these methods are powerful, they often involve randomization and probabilistic elements that make their behavior unpredictable and their outcomes difficult to interpret. The internal mechanisms of these heuristic-based algorithms are inherently complex. For instance, in deep learning, the process involves adjusting millions of parameters across multiple layers of a neural network. The non-linear activations and interconnected layers create a highly non-convex optimization problem, where the path to the solution is neither straightforward nor easily decipherable. The resulting models, though effective, operate as "black boxes," meaning that it is challenging to understand the precise way in which they arrive at their predictions or decisions. The use of randomization in optimization algorithms, such as the initialization of weights in neural networks or the random sampling of data in SGD, adds another layer of complexity. These stochastic processes help in escaping local minima and exploring the solution space more broadly, but they also contribute to the unpredictability and opacity of the optimization process.
The black-box nature of non-convex optimization models poses significant challenges for interpretability and transparency in AI. Understanding why a model made a particular decision or prediction is crucial in many applications, such as healthcare, finance, and autonomous systems. Efforts in interpretable AI and explainability aim to mitigate these issues by developing techniques that can provide insights into the model's decision-making process, even for highly complex non-convex models. The reliance on heuristics and the resultant lack of transparency can affect the reliability and trust in AI systems. Stakeholders, including end-users and regulatory bodies, need assurance that the models are functioning correctly and making decisions based on sound principles. Addressing this challenge requires ongoing research into more transparent heuristic methods and better understanding of the optimization landscapes. While heuristics enable the practical application of non-convex optimization, they are not guaranteed to find the global minimum. The efficiency and effectiveness of these methods can vary, leading to potential suboptimal solutions. Continuous improvements in optimization algorithms, such as advanced variants of gradient descent and novel heuristic methods, are essential to enhance the performance and reliability of non-convex optimization in machine learning.
In conclusion, the non-convex nature of optimization in machine learning endows models with exceptional expressive power and generalizability, especially in high-dimensional spaces. However, this complexity necessitates reliance on heuristics, which in turn transforms these models into "black boxes." The challenge lies in balancing the powerful capabilities of non-convex models with the need for interpretability, reliability, and efficient optimization, driving ongoing advancements in the field.
Conclusion
In summary, while non-convex optimization enhances the expressive power and generalizability of machine learning models, particularly multi-layer perceptrons, it also introduces significant challenges due to its reliance on heuristics, leading to "black box" models. Addressing these challenges requires ongoing research into more transparent and interpretable methods. Balancing the powerful capabilities of non-convex models with the need for reliability and transparency is crucial for their effective and trustworthy deployment across various domains.



